This post, written by Christopher M. Graney, was originally published in Sacred Space Astronomy, an online publication of the Vatican Observatory. Republished with permission.
Black holes are all in the news, with the Nobel Prize in Physics being awarded to Roger Penrose, Reinhard Genzel, and Andrea Ghez, for their work on black holes. The Faith & Science post from this past Wednesday was about Juan Martín Maldacena of the Institute for Advanced Study at Princeton University; his area of study is black holes. The video below features Maldacena talking about his work.
Roger Penrose was at the Vatican Observatory in 2017 as part of its “Black Holes, Gravitational Waves and Space-Time Singularities” conference. Fr. Gabriele Gionti, S.J., who is a scientist at the V.O., sent me the pictures below of Penrose at that conference.
From left to right: Fr. Gabriele Gionti, S.J.; Gionti and Penrose atop Castel Gandolfo; an intense side discussion.
Penrose presenting at the conference.
Since you are reading Sacred Space Astronomy, you have probably heard black holes mentioned many times. But have you heard a good explanation of what they are? “Cool” things like black holes tend to be talked about a lot, and perhaps explained not so much—indeed, sometimes they seem to be something only wizards can understand. Yet the basic ideas behind black holes are straightforward. They are not beyond the comprehension of the average person.
Consider these three basic ideas:
1. The laws of physics are the same for everyone, regardless of their “reference frame.”
Imagine you are riding in a bus that is smoothly traveling down a road, and you are holding a golf ball. You drop the ball. As you see it, the ball falls straight down to the floor of the bus and bounces. Your reference frame is that of a bus-rider. A person located on the side of the road, however, would not see the ball fall straight down and bounce straight up, because to that person the bus is moving by, and the ball is moving by with it. That person would see the ball drop and bounce, but also move by with the bus. You and the person on the side of the road would disagree about how you see the ball move. However, you would agree on the laws of physics that govern the ball’s motion. This idea is to some extent a matter of common sense.
2. The speed of light is the same for everyone.
This is a postulate of Albert Einstein’s theory of relativity. No matter how you may be moving, you will always see light travel at a speed of 186,000 miles per second, or 300,000 meters per second. No matter where you are, or what you do, or what is happening, you will always find that light travels at this speed, known as c (because it is a constant for everyone). This idea of c arose from studies of electromagnetic waves (light is such a wave) in the 19th century. For example, consider sound waves. They travel through air at a certain speed, and if you also move through the air that motion will influence how you experience those waves. So, what do light waves travel through? Einstein’s idea of c bypassed such questions.
3. There is no physical difference between gravity and acceleration.
This is another postulate of Einstein’s theory of relativity. Consider a classroom, on Earth, with only one tiny window. In that classroom, a professor is teaching about the physics of falling objects. A golf ball dropped in the classroom accelerates downward. The ball gains speed at the rate of 9.8 meters per second every second—so that one second after it is released, it is moving downward at 9.8 m/s; two seconds after it is released, it is moving downward at 19.6 m/s; etc. (A shorthand for “9.8 meters per second every second” is “9.8 m/s2.”)
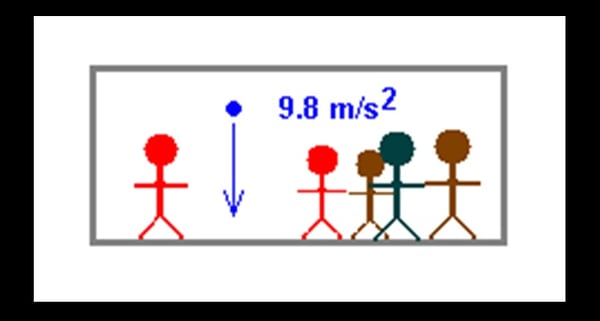
Everyone in the classroom sees the ball accelerate because the classroom is in Earth’s gravitational field, and Earth’s gravity pulls the ball downward.
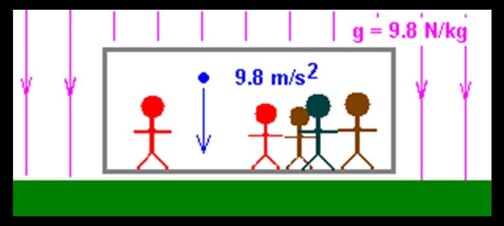
However, if the same classroom were in a rocket ship in deep space that was itself accelerating at a constant 9.8 m/s2 thanks to its engines, the students and the professor could not tell the difference between that and the Earth’s gravity. While the professor was holding the ball, it would accelerate with the ship. When the professor released the ball, it would stop accelerating and would move with constant velocity (“an object in motion remains in motion”). However, the ship would continue to accelerate, and so the distance between the ball and the floor would decrease—everyone in the classroom would see the ball “fall” to the floor as though a force was acting on it. This is just like in a car: when you step on the gas and accelerate forward, loose objects on the dashboard “fall” backward as though there were forces on them; when you step on the brake, loose objects “fall” forward.
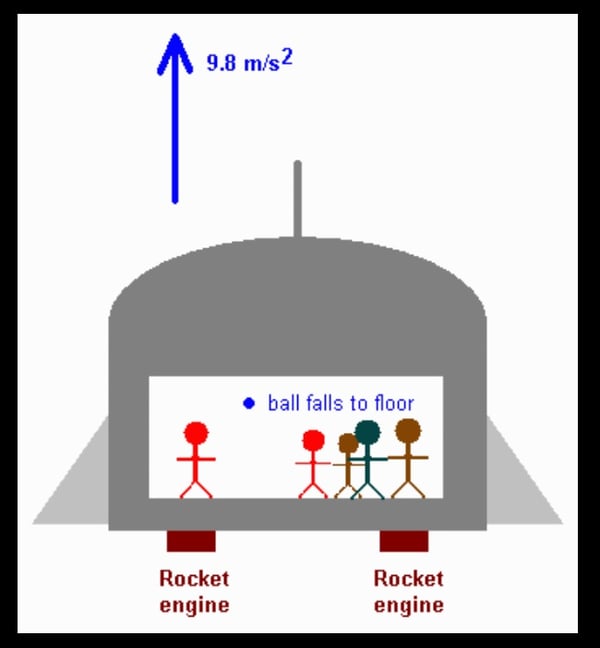The ship accelerates upward under the influence of its rockets. The ball, when released, moves at constant speed upward, but the accelerating floor rises toward and catches up with it. Thus, the people in the ship will see the ball fall to the floor with an acceleration of 9.8 m/s2.
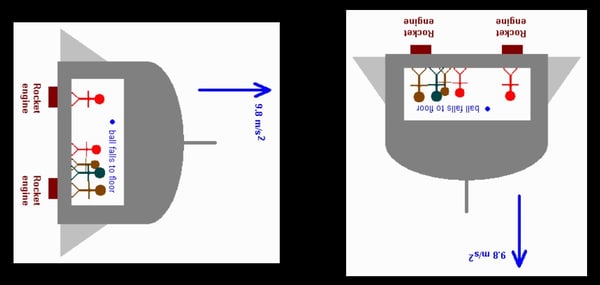
To make things perfectly clear here, this has nothing to do with which way the ship is heading. We can orient it any way we like; the ball always “falls” to the floor of the classroom in the same way. There is no up and down in space.
Arguably, this idea #3 has links to studies of electricity and magnetism, too. For example, a magnetic field has a different effect on a clay ball than on an iron ball, even if both balls have the same mass. Why is this not the case for a gravitational field? Well, mass is defined by acceleration; Newton defined mass as force divided by acceleration. Indeed, a way to determine if the clay ball and the iron ball both have the same mass is to attach each to the end of the same horizontal spring, stretch the spring and release, and see how each moves in response to the spring’s force. So, if gravity and acceleration are the same thing, that would explain why gravity acts on both balls in the same way.
A number of interesting consequences arise from this idea about acceleration and gravity being equivalent. These include gravitational lensing, gravitational red shift and time dilation, and black holes.
Gravitational Lensing
If gravity is physically identical to acceleration, then a gravitational field must act on a light beam. Suppose that, through the small window mentioned previously, a pulse of light enters the “classroom in the rocket ship.”
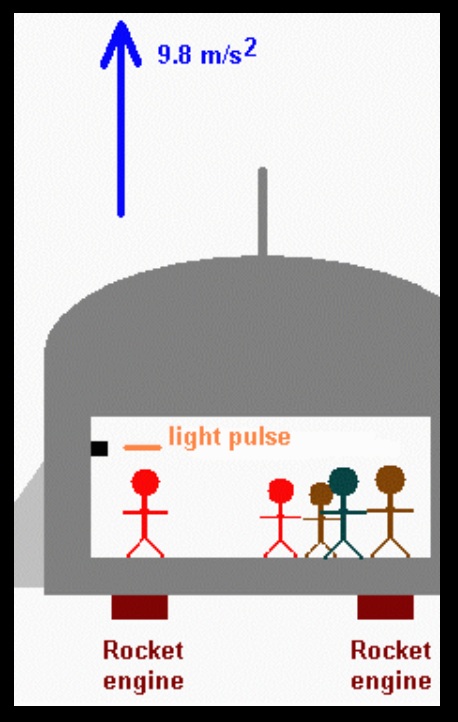
Because the ship is accelerating, the light pulse will “fall” towards the floor of the classroom at a rate of 9.8 m/s2, just like the golf ball did. The light moves so rapidly across the room that it will “fall” very, very little as it crosses the room, but nonetheless, it will “fall.” And were the acceleration of the ship great enough, the “fall” could be significant, as in the figure below.
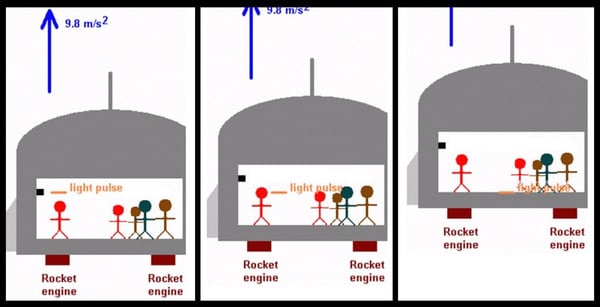Here we see that, as the rocket accelerates, the light pulse is left behind. The result is that the pulse “falls to the floor” as seen by the occupants of the ship, who cannot tell if they are accelerating or if they are in a strong gravitational field. Note that the pulse simply moves horizontally, as viewed from outside the rocket ship.
Now, if a gravitational field is identical to an accelerating reference frame, then a light pulse entering the window of the classroom in the gravitational field should also fall towards the ground. Gravity must act on light. This effect would be quite small in a classroom on Earth. However, the effect of light being deflected by a gravitational field has been well documented. The most dramatic examples of gravity acting on light are the examples of “gravitational lensing” found in astronomy. If a massive object such as a galaxy lies between an observer and a distant object, the galaxy’s gravitational field can bend light from the distant object toward the observer as shown here.
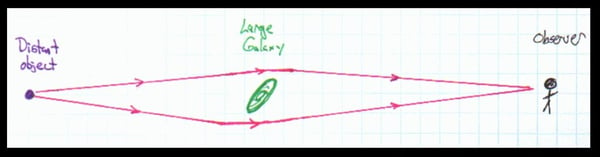
To the observer, light from the distant object seems to be coming from above and below the galaxy.
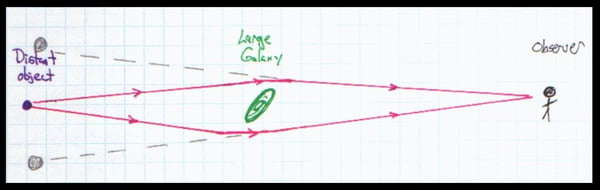
The result is that the observer sees an image of the distant object appearing above and below the galaxy. Of course, this happens in three dimensions, so images of the distant object can appear to the left and right of the galaxy as well. This is what is known as an “Einstein Cross.”
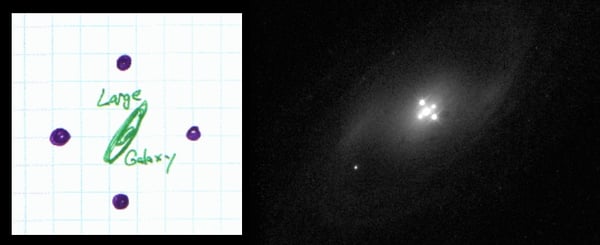Left—the bending shown in the figures above yields four images of the distant object, forming an “Einstein Cross.” Right—a real Einstein Cross.
If the alignment is just right, it is possible for light from the distant object to converge from all directions around the galaxy toward the observer. The result of this sort of unique geometry is an “Einstein Ring.” However, gravitational lensing usually doesn’t produce such neat, clean shapes. The usual result of gravitational lensing is multiple images, often distorted into arc shapes.
Left—an “Einstein Ring” caused by gravitational lensing. Right—here all the blue-colored images are all of the same object! The cluster of galaxies at the center of the picture has lensed the light from that distant object into partial rings, or arcs.
Gravity does not exert a force on light; “force” refers to something which causes a mass-having object to change its motion. Light has no mass, so “force” is meaningless in reference to it. Thus, we have to think of gravity in other ways than as a “force.” Light follows a straight-line path through space when not in a gravitational field, so we think of gravity not as a “force” but as a “warping” of space. Light wants to travel in a straight line through space, but space itself is curved by the presence of a massive object, so the light travels in a curved path. Think of water flowing through a hose. The water just wants to follow the hose. If the hose is straight, the path of the moving water is a straight line. If the hose is bent, the path the water follows is bent.
Gravitational Red Shift and Time Dilation
Launch a golf ball straight upward from Earth’s surface, and it will lose energy of motion as it rises upward in the planet’s gravitational field, and thus it will slow down. Gravity has an effect on light, just like on the ball, so light emitted straight up from a planet’s surface must also lose energy as it rises upward in the planet’s gravitational field. However, light does not slow down—remember idea #2 above. The energy of light is related to its frequency, not its speed. High-frequency (short wavelength) blue light carries more energy; low-frequency (long wavelength) red light carries less. Thus, blue light is more energetic than red. So, light sent straight up in a gravitational field will lose frequency.
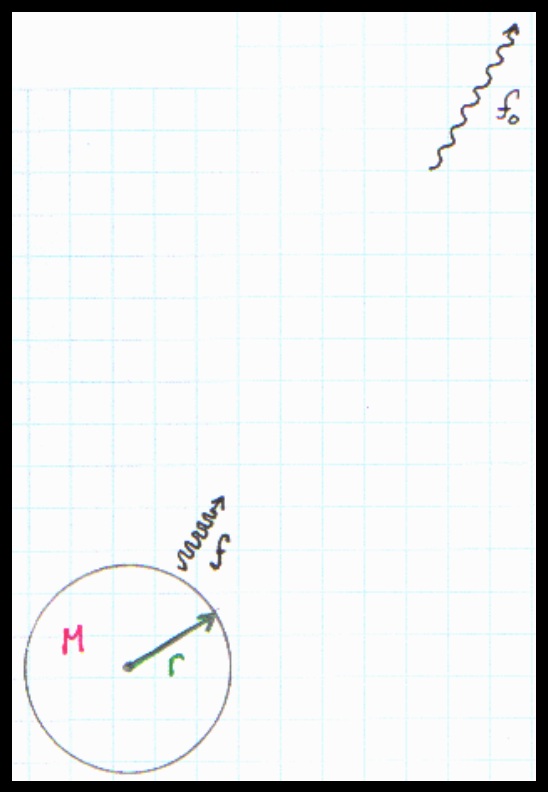
Consider a beam of light with frequency f sent up from a planet. When the light gets far from the planet (so far that the planet appears to be but a point by comparison), the frequency of the light will have decreased because the light will have lost energy, and it will have frequency f0. This change in frequency is called gravitational red shift. The name “red shift” is used because the effect tends to make blue light less energetic, longer in wavelength, and therefore redder in color.
Imagine that some astronauts who are in a ship that is far from the planet send a robotic probe down to the planet’s surface. The robot sends back a radio signal saying that it has landed. But suppose that the gravitational field of the planet is sufficiently strong to stretch the radio waves (radio is just a long-wavelength form of light) to twice their original length (so f0 = 2×f). Since the speed of light is always the same, that means the signal that the astronauts receive will be stretched to twice as long as the signal the robot sent—the wave train of the signal will be twice the length it was when sent by the robot, and it will take twice as long to cross the astronauts’ antenna as it took to leave the robot’s antenna.
Perseverance's Radar Imager for Mars' Subsurface Experiment (RIMFAX) / NASA/JPL-Caltech/FFI
The astronauts will therefore see all the actions of the probe occurring at half-speed, including the running of the robot’s clock. The astronauts will see time as running at half speed for the robot. Thus, the gravitational red shift means that there is also a gravitational time dilation. Gravity is not just a warping of space, time is affected as well. Gravity is a warping of space and time by massive objects.
Black Holes
A black hole imaged by the Event Horizon Telescope / Nasa-Event Horizon Telescope-Collaboration
Now, imagine that the planet’s gravity is so strong that the signal sent by the robotic probe loses all its energy—like an upward-thrown golf ball that comes to a halt and drops back. The wavelength of the robot’s signal is infinitely red-shifted, so that the f0 the astronauts receive is zero; indeed they receive nothing. The gravity is so strong that no signal can escape. That is a black hole. Note that the black hole infinitely stretches the signal the probe sends, so it is warping space infinitely. The black hole infinitely stretches out the signal in time, too, so it is infinitely warping time. This infinite warping of space and time means that space and time, and hence the laws of physics, as we know them, do not exist in a black hole.
Now you understand black holes. And all that, from three pretty simple ideas! The logic of black holes was worked out before there was ever any evidence that such things actually exist. But now we have pretty solid evidence that black holes do, in fact, exist.
Cover Image: The Arrhythmic Beating of a Black Hole Heart / Credit: X-ray: NASA/CXC/MPE/J. Sanders et al.; Optical: NASA/STScI; Radio: NSF/NRAO/VLA
Author Bio: Christopher M. Graney is an Adjunct Scholar at the Vatican Observatory. For some years now his research focus has been the history of astronomy, especially the late 16th and early 17th centuries. That research has resulted in two books: Setting Aside All Authority: Giovanni Battista Riccioli and the Science Against Copernicus in the Age of Galileo (2015), and Mathematical Disquisitions: The Booklet of Theses Immortalized by Galileo (2017), both published by the University of Notre Dame Press. Graney is also editor of the Vatican Observatory Faith and Science pages.
Read Also:
Dr. Vera Rubin and Why Dark Matter Matters
Black Holes, Stephen Hawking, and the Evangelical Physicist Who Proved Him Wrong