“What then is time? If no one asks me, I know what it is. If I wish to explain it to him who asks, I do not know.” -St. Augustine of Hippo, Confessions, Chapter 11
Introduction
This is the fourth in a series of articles on the nature of time. The first focused on philosophical arguments about time, the second on how we perceive time, the third on entropy, “time’s arrow.” In this piece, I’ll explain why relativity changes our view of time from an absolute dimension to one that depends on how we’re moving and where we are. The view of time as an absolute dimension was proposed by Newton and seemed reasonable until Einstein came up with his theory of special relativity over 100 years ago.
Newton and absolute space, absolute time
Before summarizing Newton’s concepts of time and space (see the Stanford Encyclopedia of Philosophy for an extended discussion), I should give some physics background to put these ideas in an appropriate context.
Let’s look at how motion and time can be related using a simple example:
A ball rolls across a billiard table. Suppose we measure the time it takes to go from the middle of the table to one foot away; let’s suppose that time is 2 seconds. Then the speed of the rolling billiard ball is distance divided by time, or ½ = 0.5 feet per second.
Now let’s suppose the billiard table is in the recreation room of an ocean liner. Let’s also suppose the liner is moving west at the speed of 50 feet per second (about 34 miles per hour). Then if the billiard ball is moving west on the table, it would be moving (50 + 0.5) feet per second west with respect to the ocean, and if it was moving east on the table it would be moving (50 - 0.5 ) feet per second west. If the billiard ball was moving north at 0.5 feet per second, perpendicular to the motion of the liner, it would still be moving west with respect to the ocean only as fast as the liner, 50 feet per second.
So we see that motion and speed are relative to a “frame of reference,” (1) that is, the motion of a given object is relative to the motion of another. We can consider the motion of the billiard ball relative to the billiard table or relative to the sea in which the ocean liner moves.
What was Newton’s ultimate frame of reference? He posited that the universe consisted of “absolute space” and “absolute time.” All motion was relative to this basic, non-moving entity. There is no way to empirically verify this notion, so one can regard it as an axio— a self-evident truth like Euclid’s axiom that parallel lines never meet. And like Euclid’s parallel lines axiom, it is contradicted by contemporary physics, as we’ll see below.
Einstein and special relativity
There is an anecdote that Einstein came upon his ideas about light speed’s constancy and time dilation while on a street car ride in Zurich (see here). That may be true, but I believe that, like most science, it was one more tier of a layer cake, with lower layers baked by Michelson-Morley, Maxwell, Lorentz, Poincare and Larmor (see here).
Nevertheless, it was Einstein who made the revolutionary suggestion in his famous 1905 paper that time was not absolute: namely, the variation of time measurements in different moving reference frames was not a calculational artifice, but a real phenomenon.
What is this “time dilation”? Einstein used a “thought experiment,” lightning bolts striking the front and back of a moving train, to illustrate qualitatively his idea. (See this video.) The basic idea is this (2):
- An observer on the platform, if the lightning bolts strike the front and back of the train just when the center of the train is in front of him, will regard the lightning bolts as striking at the same time, simultaneously, since he is in the middle of the train when the lightning bolts strike.
- An observer sitting in the middle of the moving train will see the lightning from the front before the lightning from the back, since she is moving toward the front and the distance traveled by the light from the front will be less than the distance traveled by the light from the back; remember, the speed of light is constant.
Which time, that of the platform observer or that of the train observer, is correct? Both, according to Einstein. In other words, there is no absolute time! And this assumption has been verified since then by many measurements, including satellite GPS corrections and cosmic ray measurements.
From this thought experiment one can conclude that events which are simultaneous in one frame of reference may not be simultaneous in another. Moreover, length measurements vary according to the reference frame in which the measurements take place (the Fitzgerald-Lorentz Contraction). Accordingly, there is not an absolute space—a frame at rest with respect to any other possible frame of reference. This linkage of length contraction and time dilation leads to the idea of mixed up space and time dimensions, or “spacetime.”
Spacetime, light cones, world line
In physics one searches for invariants: quantities that remain the same even when you change the way of looking at a system. In classical physics, one such invariant is the distance between two stationary points, A and B. Would there be an equivalent invariant in the new, relativistic picture?
Yes! Two years after Einstein published his special relativity paper, Hermann Minkowski proposed that spatial coordinates x, y, z and time t, could be combined in a four-dimensional spacetime; and in this spacetime there was an invariant s, the distance in spacetime. (3) Note that any representation here of that four-dimensional spacetime will have to be a two-dimensional slice of a three-dimensional slice of a four-dimensional entity—it’s very hard to visualize four dimensions, but see the illustration below.
Let’s try to visualize what this invariance means. Consider a sphere: if you move on the surface of a sphere, the spatial coordinates x, y, z will change, but the distance to the center of the sphere, its radius r, will remain constant. Similarly, if you move on the surface of a four-dimensional spacetime sphere, the spatial distance d and the time t may change, but they’ll change in such a way that the spacetime distance s from the center of the spacetime sphere is constant. (4)
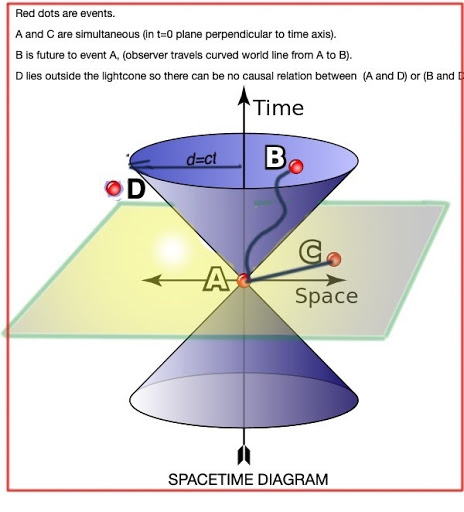
In the spacetime diagram above, the top cone represents the future and the bottom cone the past. Light travels on the cone surface; light from the past reaches event A; light from event A reaches future points. Since the speed of light is constant, independent of the reference frame, the cone surface is the same for all observers. However, within the cone, what would be the horizontal cross-section for one reference frame (observer) could be a tilted cross-section for another with a different reference frame.
Let’s think about two events, A and B, in a given reference frame in spacetime. The space distance between them is “d.” Event B occurs a time, “t,” after event A. (For example, A might be your 21st birthday and B the 30th.) Now, there is some path in spacetime—coordinates x, y, z, and time—that would be taken by the observer in going from event A to event B. This path is called a “world line.” It can be straight, it can be squiggly, whatever! If you’re moving at a constant velocity v, between the two events, the world line will be a straight line given by d=vt. See the illustration above (modified from Wikimedia Commons).
The animation below shows how events simultaneous in one reference frame are not in others.
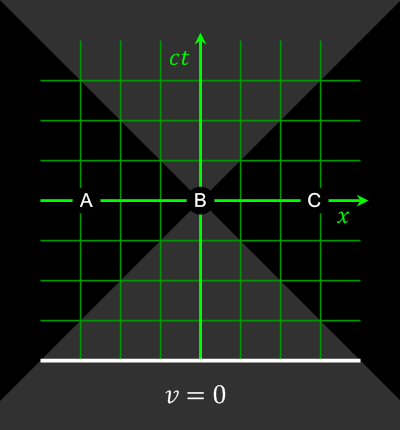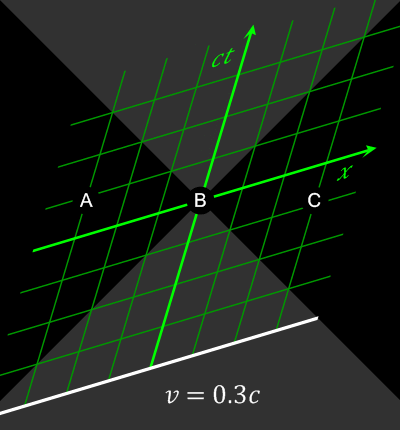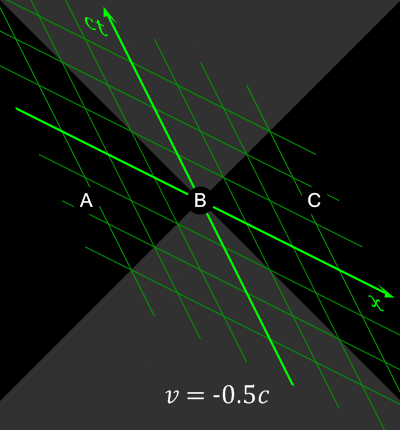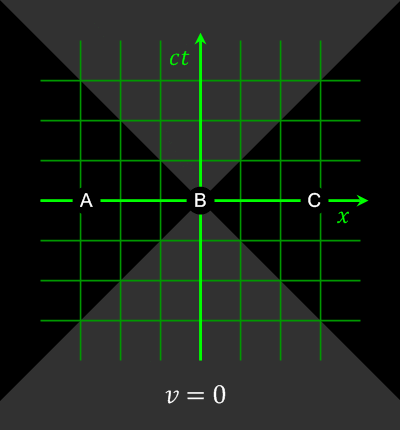 The order of events simultaneous in v=0 frame (t=0) are changed in moving frames; note: events A and C are outside B’s
light cone, so there is no causal relation between A,B,C / from
Wikimedia Commons
The order of events simultaneous in v=0 frame (t=0) are changed in moving frames; note: events A and C are outside B’s
light cone, so there is no causal relation between A,B,C / from
Wikimedia Commons
As shown in general relativity, mass distorts spacetime (see here), so the picture becomes much more complicated than that given by the illustration. Time runs slower in the presence of gravity. Thus if mass is present, it is no longer possible to take a cross-section of spacetime in which there is a constant value of t time. Indeed, as one approaches a black hole and gravity increases, time slows down. In the black hole (a singularity in space-time) with infinite gravity, supposedly time would not pass.
Causality and the block universe
The time order of events is preserved in special relativity if events lie in the same light cone. Given this condition, if event A precedes (timewise) event B in one reference frame, “it can be shown” (5) that A will precede B in all other reference frames. Thus the required time order for “A causes B” is preserved in all reference frames. Nevertheless some philosophers maintain that the lack of universal simultaneity in a light cone picture implies that all events in future and past are equally real (“have ontological status”).
If that is the case, events both future and past are set in the universe. The universe is pictured as a four dimensional block of spacetime (hence “block universe”) in which events are located at particular spacetime points.
Needless to say, it’s difficult for those of us who believe in free will to credit this picture. If future events are “there,” preordained, there seems to be nothing the individual can do to change the course of the future. We pass from one event to another, like passengers on a train controlled by an unknown engineer.
Not all physicists and philosophers agree with the block universe interpretation. Two physicists, Christopher Isham and John Polkinghorne, debated the truth and utility of the block universe at a Conference on Quantum Cosmology called by Pope St. John Paul II. The debate is summarized here. I’ll present one argument against a block universe below.
Against a block universe scientific theories change
Unlike dogma, scientific theories change with time as new data demands new theories. To credit the ultimate reality of a block universe requires one to believe current science is the only truth:
“...a physical tail to wag a metaphysical dog, to capitulate to gee-whizzery in defiance of facticity, to embrace scientism.” -Scientist B (John Polkinghorne?), “The Debate over the Block Universe” from “Quantum Cosmology and the Laws of Nature”
In other words, such a block universe requires belief beyond common sense, a new form of scientism. One hundred years from now what new theory might do away with the idea of a block universe? Indeed, present physical theory is not all that consistent with a unified view of the nature of time. The irreversibility of the real universe, entropy as “the arrow of time,” is not yet explained by the time symmetry of fundamental physics. Moreover, time in quantum theory can take on peculiar attributes that make specified spacetime locations invalid.
Forthcoming
In Part V, I’ll examine how time is manipulated in quantum mechanics, in both ordinary and fantastic fashion.
Notes and References
(1) Appropriate frames of reference for special relativity are “inertial frames,” that is to say, frames of reference moving at a constant velocity. I’ll let the term “inertial” be understood in what follows.
(2) See here for a video describing this in more detail.
(3) The invariant spacetime distance is s2 = d2 - (ct)2, where d is the spacelike distance between two points (spacetime “events”), c is the speed of light, and t is the time dimension parameter. See this video for a more detailed explanation.
(4) Here’s how to define accessible points in spacetime. Suppose you have light emitted from a point source at a time t, which we’ll take to be t=0, the present. Light will travel in various directions from that point. At some time t (in your reference frame) the light will have traveled a spatial distance d=ct. In three spatial dimensions this would be a sphere, radius d=ct. In four dimensional spacetime, lines d=ct form the surface of a cone, as in the illustration below. The cross-section of a four-dimensional cone would be this sphere, radius d=ct. In the illustration, a one-dimensional perspective (ellipse) of a two-dimensional slice (circle) of this three dimensional sphere is shown, with radius d=ct. For you, the observer at A when the light was emitted at t=0, simultaneous events lie in planes perpendicular to the t axis.
(5) See here for a short justification of this claim. It depends on spacetime distance between two causally related events being “timelike,” rather than “spacelike.” That corresponds to spacetime distance, s2 being negative (s being imaginary).
Read Also:
What is Time? Part I—Philosophy

